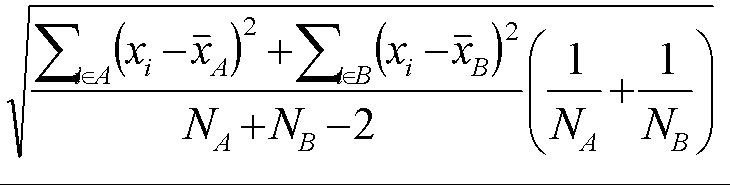
Kétmintás t-próba (Student's t-test)
A segédprogramot Tarczay Klára írta.
A matematikai háttér:
Elég gyakori probléma, hogy szeretnénk tudni, két
eloszlásnak vajon ugyanaz-e az átlaga. Például:
az elsõ mért adatok olyanok, melyek egy esemény elõtt
történtek, a második mért adatok pedig az esemény
után lettek összegyûjtve. Ezek után kíváncsiak
vagyunk, hogy az esemény - "kezelés" vagy a "kontrollparaméterek
változtatása" - okozott-e változást. Egy egyszerû,
szemléletes példa erre: meteorológiai állomást
építenek a város szélére, majd néhány
év elteltével a város terjeszkedése során
az állomást is körbeépítik. Befolyásolta-e
ez a tény az adatokat, és mennyire szignifikáns a hatása?
Az elsõ gondolatunk az lehet, megkérdezzük, hogy a két
összegyûjtött adatsor átlagának mennyi a szórásnégyzete.
Hasznos dolog tudni ezt a számot: megmutatja az átlagok különbségének
az "erõsségét vagy fontosságát",
ha ez a különbség jelentõs. Mindezek mellett nem mond
semmit arról, hogy az adatsorok mennyire különböznek,
azaz statisztikailag szignifikáns-e az eltérés. Az átlagok
eltérése elõfordulhat, hogy semmi összefüggést
nem mutat a szórásnégyzettel, miközben az eltérés
akár elég nagy is lehet. Ez akkor áll fenn, ha sok adatunk
van. Fordítva, a különbség mérsékleten
nagy lehet, de nem szignifikáns, ha "ritkák" az adatok.
A mennyiség, ami méri az átlagok különbségének
"nagyságát", nem a szórásnégyzet
(standard deviation), hanem az ún. standard hiba (standard error). Az
adatok értékének standard hibája megmutatja, hogy
az adatokból nyert átlag mennyire pontosan becsli a "valódi
átlagot". A standard hiba jellemzõen megegyezik a szórásnégyzet/adatpontok
számának négyzetgyökével.
A szokásos statisztika arra, hogy az átlagok eltérésének
szignifikanciáját mérjük, a kétmintás
t-próba. Itt meg kell jegyezni, hogy csak abban az estben alkalmazhatjuk
ezt a próbát, ha normál eloszlású minták
paramétereire vonatkozik a próba, és a minták függetlenek.
Akkor használjuk, ha úgy gondoljuk, hogy a két mintának
a szórása megegyezik, de az átlaguk lehet, hogy nem. A
t-próbát a következõképpen számítjuk:
1. A standard hibát megbecsüljük az átlagok különbsége
és a korrigált tapasztalati szórásnégyzet
alapján az alábbi formulából (Sd):
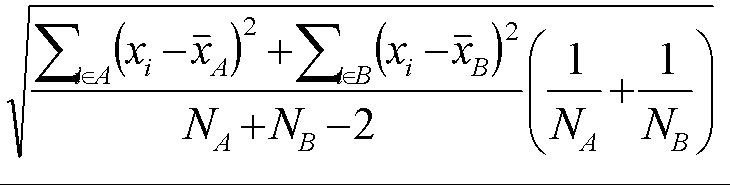
ahol az egyes szummákat az adott adatsor adatszáma szerint kell venni, NA és NB az egyes adatok száma, és az adatsorok átlaga.
2. Kiszámítjuk a t-próbát (t):
3. Összehasonlítjuk a t-próba értékét
az NA+NB-2 szabadsági fokú Student-eloszlás adott
biztonsági szinthez tartozó értékével, majd
külön subroutine-nal becslést adunk a szignifikancia értékére.
Ennek tárgyalásába most nem megyek bele. Itt azt kell csak
tudni, hogy a "nem teljes" (incomplete) béta függvényrõl
szóló programrészletet alkalmazza a számítások
során a subroutine.
A szignifikancia egy 0 és 1 közötti szám, és
valószínûség, hogy az viszonylag nagy is lehet, még
ha a kifejezések átlaga meg is egyezik. Így a szignifikancia
numerikus értéke ha kicsi ( 10-3), az azt jelenti, hogy az észlelt
különbség nagyon jelentõs. Fontos megemlíteni,
hogy a statisztikai biztonság minden esetben 95%-os.
A subroutine használata:
A subroutine bemenõ adatai, vagyis amit meg kell adni: a két
adatsor egy-egy vektorban tárolva és az adatsorok elemszáma
-data1, data2 a két vektor (valós), n1,n2 a két elemszám
(egész).
A kijövõ értékek: t- a t-próba értéke
(valós) és a prob nevû (valós) szám, amely
megmutatja a szignifikanciát.
A programrészlethez szükséges még egy subroutine:
avevar -ez számítja az átlagokat és a szórásokat;
és egy függvény: betai - ez pedig a hipotézisvizsgálathoz
kell. A betai függvény felhasznál további két
függvényt: betacf
és gammln.
A subroutine meghívása:
A subroutine-t a következõ módon kell meghívni a fõprogramban:
call ttest(data1,n1,data2,n2,t,prob)
Megj.: Érdekes lehet gyakran az is, hogy mennyi a minták átlaga és szórásnégyzete. Mivel ezt is kiszámolja a subroutine, ki lehet íratni.
Példa a segédprogram használatára:
program teszt
parameter (n=3)
real data1(n),data2(n)
data data1/290,311,284/
data data2/271,304,260/
call tptest(data1,data2,n,t,prob)
write(*,*)t,prob
stop
end
Fontos! A data adatmezõt a programszövegben kell módosítani, tehát nem input adat!!!!
Ha ezekkel a számokkal futattod le( data1/290,311,284/ illetve data2/271,304,260/ , ezt kell kapnod: 3.304... és 0.0806...
Itt leled e hasznos segédprogramot: tproba.for