Az adatok digitális tárolási módja

Mint minden digitális eszköznél, így a számítógépek esetében is az információ tárolása 2-es számrendszerbeli számok segítségével történik, melynek alapegysége a bit (0 vagy 1 értékkel). Így van ez ma már a műholdak adattovábbítása során is, ahol a régi analóg technológiát váltotta fel a digitális képátvitel. A digitális technikában a biteket valamilyen szabvány szerint csoportosítani szokták, ennek megfelelően alkothat 8, 10, vagy 16 bit egy egészet, amely a számítástechnikában a szó nevet viseli. A napi gyakorlatban használt számítógépek 8 bitet tekintenek egy egységnek, s ezt nevezik 1 bájtnak. A mindennapokban használt IBM kompatibilis személyi számítógépek, a UNIX alapú munkaállomások (Silicon Graphics, HP, IBM, Sun, stb.), valamint a Macintosh számítógépek is az egész vagy valós számokat a megkövetelt pontosságtól függően egy bájton, vagy annak többszörösén tárolják. A számítógépes programnyelvek (pl. FORTRAN) adattípusai egységesen ennek megfelelően lettek kialakítva (pl. az egyszeres pontosságú valós számot 4 bájton, a dupla pontosságú valós számot 8 bájton tárolunk).

A NOAA műholdakról sugárzott adatok bináris szerkezetüket tekintve 10 bites formátumúak, vagyis 10 bit felel meg egy szónak, tehát egy tízes számrendszerbeli szám 10 biten van kettes számrendszerbeliként tárolva. Például a tízes számrendszerbeli 644, 2-es számrendszerben 1010000100-ként írandó. Ezen a 10 helyiértéken a 0-tól 1023-ig terjedő egész számok tárolhatóak csak el (2**0+2**1+2**2+2**3+2**4+2**5+2**6+2**7+ 2**8+2**9 = 1023 = 2**10-1). Megállapodástól függően akár a -512-től 511-ig terjedő intervallum számait is tárolhatnánk ezen a 10 biten, a definiált intervallum a tárolt mennyiséghez van igazítva. A 8 biten való adattárolás ugyanezt csak 0-tól 255-ig (2**8-1) engedélyezné, a 16 bit esetében pedig 0-tól már 65535-ig (2**16-1). Míg az első nagyon kevés információ tárolására alkalmas, addig az utóbbi már túlságosan sokra. 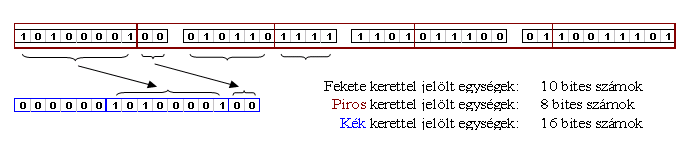De a műholdakon levő műszerek felbontóképessége a távolság miatt a 16 bites tárolást már nem igényli.
Az adattovábbítás rendszerének kiépítésekor egyrészt gondolni kellett arra, hogy minél rövidebb legyen az a fájl, mely a műholdról kisugárzásra kerül, másrészt pedig alkalmas legyen elegendő információ továbbítására. Így született meg az a kompromisszum, hogy egy számot 10 biten tároljanak, és így küldjék le a Földi vevőállomások felé.

Mivel a PC-k, munkaállomások és egyéb számítógépek a 8 bites információtárolási rendszeren alapulnak, ezért a nyersen érkező fájlokat át kell konvertálni a 10 bitesről 8 bites formátumba. A közvetlen 1×8 biten való tároláskor információvesztés lépne fel, így ennek elkerülésére a 16-bites verziót kell használni. Ezzel ugyan megnő a fájl mérete, de a vevőállomáson ez már nem jelent problémát. A konverzió az 1. ábrán bemutatott módon történik. 4 darab 10 biten alapuló számot kezelünk egyszerre, mert (4·10) = 40 a legkisebb közös többszöröse a 8-nak és a 10-nek. Az ábrán fekete kerettel jelölt egységek az eredeti szavak, a piros keretűek pedig a számítógéppel beolvastatott forma. Minden 16 bites egység első 6 bitje értelemszerűen 0 lesz. Az első 16 bites egység első 6 darab 0 karaktere után csatoljuk ezen túl még az első 8 bites egységet, illetve a maradék 2 bitre a második 8 bites egység első 2 bitjét tesszük. A fennmaradó 6 bitet a második 16 bites szám első 6 darab nulla karaktere után tesszük, melyet még 4 bit követ a harmadik 8 bites számból. Mire az ötödik 8 bites egység végére érünk értelemszerűen a 10 bites számok is elfogynak, előállítván így a 16 bites számokat, melyeket már tudunk kezelni. Ezzel a módszerrel miden nyers, a műholdképről érkező fájlt át kell konvertálnunk 16 bitessé az eredeti 10 bites formátumból.

1. ábra
A konvertálás sematikus módja

A fájlok szerkezete

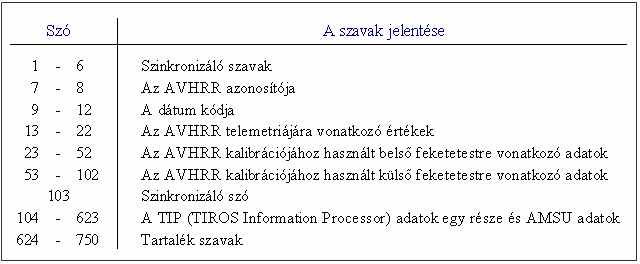
A „HRPT” módszerrel a Földre továbbított fájlok szerkezete minden esetben azonos. Ezekben a fájlokban a bináris értékek egymás után, mindennemű tagolás nélkül folytonosan következnek. Ahhoz, hogy a számunkra szükséges információkat kivehessük, meg kell ismernünk az adatok szerkezetét. Az AVHRR sugárzásmérő műszer a műhold haladása közben soronként letapogatja a földfelszínt. Egy soron való végighaladás a másodperc tört része alatt történik (megközelítőleg 0,16 másodperc), mely időtartam alatt egyik pályaparaméter sem változik lényegesen. Így mindig az adott sor letapogatásának kezdőidőpontját tekinthetjük az egész sorra érvényesnek, s ezt az időpontot rendelhetjük hozzá az adott sorban a műszerek által mért minden értékhez. Ugyanez vonatkozik a különböző pályaelemekre és a kalibrációs konstansokra is. Így ezen információkat elég soronként frissíteni, minek következtében minden sorkezdet esetén először egy 750 számból álló ún. headerrel, azaz fejléccel találkozunk. Ezen fejlécek szerkezete egységes (3. táblázat). A táblázatból kitűnik, hogy amennyiben csak az AVHRR képeit szeretnénk feldolgozni, és például a vertikális szondázás eredményeivel nem, akkor a fejlécekből csak az első 103 szóra van szükségünk.

3. táblázat
A HRPT fájlok fejlécének szerkezete

A fejléc után következnek az úgynevezett „Földadatok”, vagyis az AVHRR műszer által mért sugárzási értékek pixelenként. Egymás után nem két egymás melletti pixel értékei állnak közvetlenül, hanem pixelenként az adott pixel mind az 5 AVHRR csatornára vonatkozó értékei. Ezt hívják BIP (Band Interleaved by Pixel) tárolási módnak. Egy sor 2048 darab pixelből áll, így ez összesen 5·2048 = 10240 darab sugárzási érték soronként. Ezek után még 100 darab egyéb, a szinkronizációhoz szükséges szó áll. A fenti szerkezetet illusztrálja a 4. táblázat.

4. táblázat
A HRPT fájlok szerkezete (1 sorra vonatkoztatva)

Minden teljes letapogatott sor után, vagyis 11090 darab szó után 7 felesleges bájt áll, mely a vevőállomásra jellemző érték. Ezután következik az újabb sor, mely ismét a fent leírt szerkezettel rendelkezik, s a fejléccel kezdődik.
Az AVHRR műholdképek a fent vázolt struktúra alapján így mindig azonos oszlopszámúak, csak soraik száma változó. A sorok száma ugyanis függ az adattovábbítás sikerességétől, illetve attól, hogy a horizont közelében pontosan hol, hány fok közelében tűnik el a műhold a földi vevőberendezés látóköréből. Ha nem létezne sem domborzata, sem légköre bolygónknak, akkor horizonttól horizontig követhetnénk a műholdakat (NOAA-15, -16, -17), melyek AVHRR műszere átlagosan kb. 5677 (= 2·2838,6) sort tapogathatna végig (2. ábra). Lapultsággal rendelkező bolygónk esetében ez nyilván a földrajzi szélességtől függő érték. Mivel ez a feltételezés nem igaz, hiszen bolygónk rendelkezik légkörrel és domborzattal, ezért gyakorlatilag azt mondhatjuk, hogy kb. 5°-os magassági szögtől tekinthető a vétel minőségileg elfogadhatónak (Tänczer, 1988).

2. ábra
A műhold által letapogatott maximális tartomány, melyről képes továbbítani
az adatokat a földi vevőállomásnak

Az AVHRR műszerrel mért adatok nyers megjelenítése

A megismert fájlszerkezet alapján összerakhatók az AVHRR műszer által mért sugárzási értékek csatornánként egy-egy képpé. Mint a legtöbb számításunkat, így ezt a megjelenítést is egy IDL nyelven írt program segítségével hajtjuk végre. A beolvasott kép legegyszerűbb ábrázolására példa a 3. ábra. Ez a NOAA-17 2003.07.22 09:31-es áthaladásának 2-es csatornája, fekete-fehér megjelenítési módban. 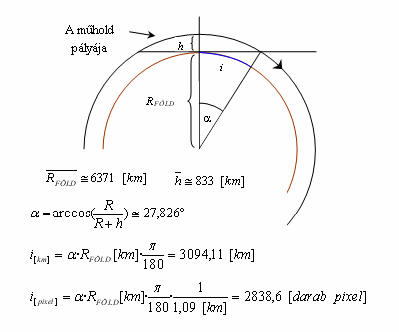Jól kivehető, hogy mivel a műhold szenzora a letapogatott gömbfelületet egy síkra képezi le, ezért a kép szélén torzulás lép fel. Ezt egy egyszerű geometriai művelettel korrigálhatjuk (4. ábra, ugyanarra az áthaladásra), azonban hangsúlyoznom kell, hogy ez pusztán az ilyen jellegű megjelenítéseknél alkalmazható, mert ilyenkor a kép szélén levő pixelek torzulnak (ld. 6. ábra). A korrekció matematikai alapja egy hengerfelületnek trigonometrikus összefüggések segítségével történő leképezése. Ezeken a képeken megfigyelhető az ún. becsillanásnak nevezett jelenség is. Ez a kellően sima vízfelszínek esetében jelentkezik, képeinken a Földközi-tenger középső, keleti részében rajzolódik ki, a Jón-tengernél, a környezetüknél világosabb pixelek formájában. A jelenség a szélcsendes időjárás hatására létrejövő szinte tükörsima vízfelszínnek köszönhetően alakul ki.

3. ábra Nyers kép / NOAA-17, 2003.07.22 09:31, 2-es csatorna/

4. ábra Geometriai korrekcióval módosított, saját színezésű kép / NOAA-17, 2003.07.22 09:31, 2-es csatorna /

A nyers képek megjelenítéséhez tetszőleges színskálát választhatunk, akár általunk készítettet is. Ennek alapja az, hogy a pixeleken tárolt értékek tulajdonképpen nem mások, mint az AVHRR sugárzásmérő műszer által mért beütésszámok, melyekhez tetszés szerint hozzárendelhetünk bizonyos színeket. Így készült egy saját készítésű színskála segítségével a már bemutatott 4. ábra, melyen a geometriai korrekciót is szemléltettem. Az egyik szokványos, gyakran alkalmazott színezési eljárás az ún. „valódi színezéssel” készített kép (True color), melyet RGB színkeverési módnak (Red-Green-Blue) is szoktak nevezni. Ekkor 3 különböző csatorna egybevetésével úgy készül a kép, hogy mindegyik csatornához különböző színt, azaz ennek lineáris skáláját rendelik (a 0-hoz a legsötétebb árnyalatot, az 1023-hoz pedig a legvilágosabbat). Vagyis az 1-es, első látható csatornához a pirosat, a 2-es, második látható csatornához a zöldet, a 4-es, második infravörös csatornához pedig a kék színt rendeli. Majd pedig ezeket a 3 csatornából eredő színértékeket egy pixelen ábrázolják (innen a név: RGB színkeverés). Erre példa az 5. ábra, mely a korábbi ábrákon szereplő áthaladásra mutatja a geometriai korrekció utáni ún. true color képet. Ezzel a megjelenítéssel a zöld különböző árnyalatiban játszik a talaj, sötétkékben a szabad vízfelszín, fehérben a nimbostratus és a cumulonimbus, világos kékes-lilában a cirrus felhők és sárgában az altocumulusok. Ezentúl e megjelenítési forma a többi felhőfajta megkülönböz-tetésére is sokkal jobban alkalmas, mint egy egyszerű fekete-fehér színskála.

5. ábra
Geometriai korrekcióval ellátott
"True color" színezésű kép
/ NOAA-17, 2003.07.22 09:31/