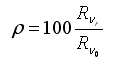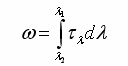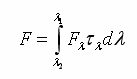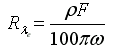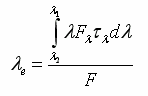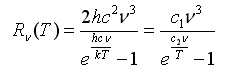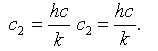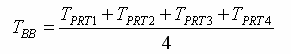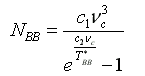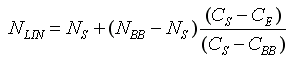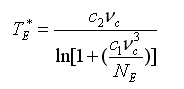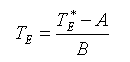A műholdak sugárzásmérő berendezéseinek kalibrációja azoknak az átviteli függvényeknek meghatározásából áll a műszer minden leképező csatornájára, melyek a beütésszám, vagyis a mért és a tényleges sugárzási értékek spektrális eloszlása között létesítenek kapcsolatot. Az átviteli kapcsolat függ a sugárzásmérést végző rendszer hőmérsékletétől és a kalibrálni kívánt csatorna hullámhossztartományától. Az a hullámhossztartomány, melyben a leképezés történik, alapvetően meghatározza a matematikailag leszármaztatható fizikai paraméterek körét. A látható és közeli infravörös tartományból származó adatokból a Föld felszínének illetve a felhőzetnek az albedója számítható, míg a távolabbi infravörös tartományból ezek hőmérsékletére következtethetünk vissza (Tänczer, 1988).

A kalibráció minden mérőberendezés esetén három fő részből áll:
(1) A műhold fellövése előtti ún. előkalibráció, mely során előkészítik a rendszert a folyamatos és operatív működésre. Ebben a szakaszban minden csatornára meghatározzák a kalibráció pontosságát, a műszer érzékenységét, a korrekciós tényezőket, valamint a kalibrációhoz szükséges lineáris és nem-lineáris paramétereket. Az AVHRR berendezéseket a műhold felbocsátásáig rendszeresen kalibrálják, legalább évente egyszer. A legutolsó kalibrációt közvetlenül a pályára-állítás előtt végzik.
(2) A fellövés utáni, világűrbeli működés közben végzett folyamatos kalibráció, mely során pontosítják az előkalibrációt.
(3) Műszaki kiértékelés, mely során a működés közben tapasztalt problémákra és szokatlan értékekre keresnek magyarázatot.
A látható csatornák kalibrálása halogén lámpák segítségével történik a műhold fellövése előtt, és közel állandó reflektanciájú területek (pl. sivatagok) felett mért sugárzási adatok folyamatos nyomon követésével a műhold pályára állítása után. A sugárzási spektrum infravörös tartományában különböző hőmérsékletű abszolút fekete testek alkalmazásával hajtják végre a kalibrációt mind a földi laboratóriumban, mind a világűrben. Mivel a műhold tényleges működési környezetét a földfelszíni laboratóriumi feltételekkel nem tudják tökéletesen előállítani, így az előkalibrációval meghatározott sugárzástani karakterisztikák nem lesznek megfelelő pontosságúak a fellövés után. Így válik szükségessé, hogy működés közben alkalmazott módszerekkel módosítsák a kalibrációt.

Ahogy a műholdakról származó sugárzástani információk egyre fontosabbá válnak a kutatásokban, úgy nő az igény a műszerek minél pontosabb kalibrációjára (Cracknell, 2001). Ezen a pontosságon erősen múlik például a légkör energiaháztartásának feltérképezése, a légköri ózon és aeroszol mennyiségének megállapítása vagy a globális éghajlatváltozással járó felszíni hőmérsékletváltozások meghatározása.
Az általunk alkalmazott és a következőkben bemutatott kalibrációs eljárás a NOAA-KLM User’s Guide legfrissebb verzióján (Goodrum et al., 2004) alapszik. A számításokhoz szükséges konstansokat részben ebből a dokumentációból, részben egyéb még ennél is frissebb internetes forrásokból használtuk fel (NOAASIS, 2004). Az eljárást beprogramoztuk, így az bármely képre alkalmazhatóvá vált.

A látható és a közeli-infravörös csatornák kalibrálása

Elsőként az AVHRR/3 műszer 1-es, 2-es és a 3A jelű csatornájára vonatkozó kalibrációt részletezzük. Az 1-es csatorna méréseit a felhőzet azonosítására és az albedó meghatározására használjuk. A 2-es csatorna adatai a felhőzet azonosításán kívül a szárazföld és az óceán szétválasztására alkalmazhatóak. A 3-as csatorna kizárólag nappal üzemelő változatának (3A) segítségével a hó- és jégtakarót tudjuk elkülöníteni a felhőzettől, valamint az aeroszolok koncentrációjának meghatározásra nyílik lehetőség. Mivel a fenti csatornákhoz tartozó hullámhossz-tartományokban az operatívan működő műszer csak a Föld által visszavert napsugárzást képes érzékelni, ezek a számítások kizárólag a nappali mérésekre végezhetők el, vagyis azokra, melyeket azon áthaladások során mért a műszer, amikor a felszínt a Napból érkező direkt vagy szórt sugárzás érte.
Ezen csatornák kalibrációját két szakaszra bontjuk az alapján, hogy a műszer üzembe állítása, vagyis a műhold fellövése előtt vagy után történik-e a műveletsorozat.

Kalibráció a műhold fellövése előtt

Az említett három csatornát a műhold pályára állítását megelőzően egy több, mint húsz év alatt kidolgozott eljárásnak megfelelően kalibrálják. A kalibrációhoz egy 102 cm átmérőjű mérőgömböt használnak, mint fényforrást. Ez a gömb több különböző teljesítményű égővel van felszerelve, melyek gyűrű formában helyezkednek el. A gömböt elhagyó sugárzás erőssége három nagyságrendű tartományban változtatható az égők különböző kombinációját alkalmazva. A különböző csatornákban érzékelő szenzorok mindegyikét megvilágítják a gömbből kilépő sugárzás különböző fokozataival, majd a sávszélességeknek megfelelően integrálják a beérkező sugárzást.

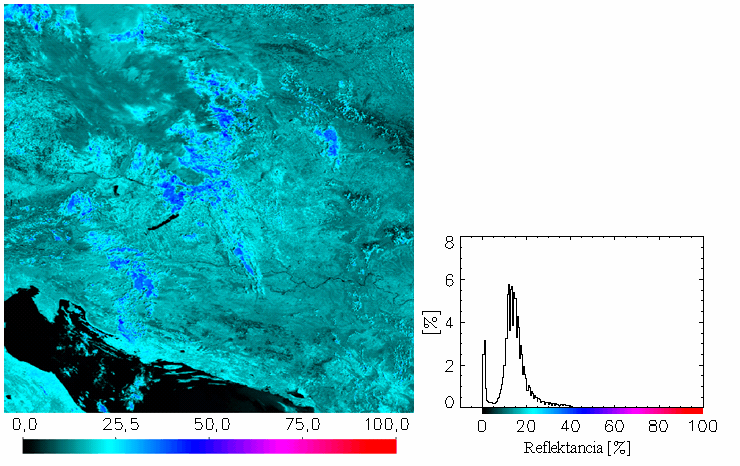
Ha a maximálisan sugárzó gömbről Rv0 értékű állandó radiancia (sugársűrűség) érkezik, a különböző mértékben sugárzó gömbökről pedig Rvr nagyságú, akkor egy egyszerű analógiát feltételezve kiszámolható a Föld felszíni reflektanciája: a laboratóriumi méréseknek a világűrben mért értékeket feleltetjük meg. Ekkor Rv0 megfelel annak a Napból eredő, rövidhullámú direkt és szórt sugárzásnak, mely a Föld felszínét (avagy a felhőzet tetejét) eléri, és Rvr képviseli ennek azt a részét, melyet a felszín és a felhőzet illetve a levegőrészecskék vernek vissza. A meteorológiai értelemben használt albedó fogalom a napsugárzásra, mint egy nagy sávszélességű (0,3-3 mikrometer) elektromágneses sugárzásra vonatkozik, ahol a beeső sugárzásáram a teljes felső, a visszavert sugárzásáram pedig a teljes alsó térfélből ered. Ez a planetáris albedó definíciója (Péczely, 1979). Ezzel szemben a sugárzásmérő műszerek csatornái csak egy korlátozott sávban mérnek, és amit érzékelnek, az csak az egy adott irányba (a műhold irányába) visszaverődő sugársűrűség. Ebből csak a reflektancia számolható, ha más hatásokat nem tekintünk. Ha a felszín ún. Lamberti visszaverő, vagyis az általa visszavert sugárzási áramsűrűség irányfüggetlen, továbbá feltételezzük, hogy a mérés hullámhossztartománya reprezentatív a napsugárzás felszín által visszavert részére, csak akkor lesz a meteorológiai albedó és a Pi-vel, vagyis 180° térszöggel megszorzott reflektancia egyenlő. (A műholdképeket feldolgozó kutatók gyakran élnek ezzel az egyszerűsítő feltételezéssel, s albedónak nevezik megtévesztően azt a reflektanciát, melynek számítását a következőkben leírtak szerint végezhetjük el.) A ro reflektancia (%) a következő képlet segítségével számolható ki:

(1)

A műszer által felfogott, a mérőgömbről érkező sugárzás jeleit rögzítik és 10 bites rendszerbe átkonvertálják. Rendszerint az AVHRR jelei nagyon közel állnak egymáshoz, ha az azt kiváltó sugárzás a teljesen kivilágítatlan gömbről és az űrt utánzó célról (mely lényegében abszolút fekete testként fogható fel) jut a műszerbe. A gömb spektrális jeleit bizonyos időközönként szintén rendszeresen kalibrálják, melynek bizonytalansága így nem haladja meg az 5 %-os nagyságrendet. Az AVHRR fellövés előtti kalibrációjának körülményeiről közöl további részleteket Rao (1987).

Az így nyert kalibrációs eredményeket a NOAA egy egyszerű lineáris regressziós kapcsolat formájában adja meg a pixelenként mért 10 bites AVHRR jel (beütésszám) (C10) és a reflektancia (ro) között a megvilágítottság különböző szintjeiben. Ezt fejezi ki (2), ahol S a lineáris egyenes meredeksége, vagyis reflektancia/beütésszám, I pedig az ordinátatengellyel képzett metszéspont:

(2)

Az S és az I konstansok (csakúgy, mint minden további konstans) csatornánként mindegyik működő NOAA műholdra hozzáférhetők (Goodrum et al., 2004). Ezeknek a konstansoknak és a (2) képletnek a használata operatívan működő műholdak esetében azzal a feltételezéssel jár, hogy a laboratóriumokban megállapított kalibrációs konstansok igazak a már a pályáján haladó műhold műszerére is. Ezeknél a rövid hullámhosszú csatornáknál annál nagyobb a beütésszám, minél nagyobb a hozzátartozó célterület reflektanciája, azaz a sugárzás visszaverődését kifejező együttható.

Az AVHRR/3 sugárzásmérő műszer egyik lényeges tulajdonsága, hogy a látható és a közeli infravörös tartományban az alacsonyabb reflektancia-értékeket finomabb felbontásban képes érzékelni, mint a magasabb reflektanciákat, vagyis a skála nem egyenletes felosztású. A 9. táblázatból leolvasható, hogy az 1-es és a 2-es csatorna esetében például ugyanannyi beütésszám jut a reflektancia-tartomány első 1-ének kifejezésére, mint a maradék 3-ére.

9. táblázat
Az AVHRR/3 sugárzásmérő műszer reflektanciára vonatkozó érzékenysége

Ez a tény szükségessé teszi, hogy a két tartományt külön-külön kezeljük, vagyis csatornánként más S és I konstansokat használjunk a kicsi (<=500) és a nagy (>500) beütésszámokhoz. Ez az 500-as beütésszám-határ csak egy kerekített, elméleti érték, a pontos értékek műholdankénti meghatározása a műhold fellövése utáni kalibráció tárgykörébe tartoznak, melyről a következő alfejezetben olvashatunk.
A reflektanciaszámítás eredményeként előálló képek (%-ban kifejezve) és a hozzájuk tartozó hisztogramok láthatók a következő ábrákon, csatornánként a NOAA-17-es műhold 2003. július 22-ei 09:31 órás áthaladására (16-18. ábra). A hisztogramokon az adott képi pixelek 0,5 reflektancia-értékenkénti csoportosításban kerültek ábrázolásra relatív gyakoriságuk (%-ban kifejezve) függvényében. Azért, hogy a képek egymással összehasonlíthatóak legyenek, ugyanolyan skálabeosztással kerültek ábrázolásra. Az ábrák segítségével tanulmányozható a műszerek érzékenysége. Az 1-es csatorna képe a felhőzet túlnyomó részét megjeleníti azáltal, hogy az ebből a csatornából származtatott értékek állnak legközelebb a tényleges reflektancia-értékekhez, így a sugárzást leginkább visszaverő képi elem, a felhőzet könnyen elkülöníthető. A szabad vízfelület és a szárazföld legjobb elkülönítésére a 2-es, és a 3A csatorna szolgál. Tekintve, hogy a példaként bemutatott felvétel nyáron készült, ezért nem alkalmas arra, hogy a 3A csatorna felhőzet és hótakaró elkülönítő-képességét tanulmányozhassuk.

16. ábra
Kalibrációval kapott reflektanciakép az AVHRR 1-es, látható csatornájából (0,58-0,68 ?m) és a hozzátartozó hisztogram / NOAA-17, 2003.07.22 09:31, 1-es csatorna /

17. ábra
Kalibrációval kapott reflektanciakép az AVHRR 2-es, látható csatornájából (0,725-1,00 ?m) és a hozzátartozó hisztogram / NOAA-17, 2003.07.22 09:31, 2-es csatorna /

18. ábra
Kalibrációval kapott reflektanciakép az AVHRR 3A, közeli infravörös csatornájából (1,58-1,64 ?m) és a hozzátartozó hisztogram / NOAA-17, 2003.07.22 09:31, 3A csatorna /

A műholdas távérzékelési mérések nagymértékben függnek a Nap, a felszíni célpont és a sugárzásmérő szenzoregymáshoz viszonyított geometriai elhelyezkedésétől, hiszen a legtöbb felszíntípus anizotrop sugárzásvisszaverő (Kriebel, 1978; Kimes et al., 1984; Kimes and Sellers, 1985; Middleton, 1991). Az AVHRR sugárzásmérő ±55,5 fokban mérhet a nadírhoz képest, s ennek következtében az áthaladástól függően ugyanaz a célpont sok különböző szögből lehet látható. Így az anizotropitás hatása miatt ugyanakkora besugárzás esetén különböző mértékű visszaverődő sugárzásokat detektál, mely lényegesen befolyásolja egy kiszemelt cél időbeli fejlődésének nyomon követését (Gutman, 1991).

Ha a felszín sugárzástani szempontból nem izotróp, akkor az előzőekben bemutatott módszerrel kiszámított reflektancia csak abban az esetben tekinthető a tényleges albedónak, ha a Nap és a műhold a méréskor a zenitben volt és a Nap-Föld távolság pontosan egy csillagászati egység (149,6 millió km). Ez a három feltétel ritkán teljesül akár együtt, akár külön-külön, ezért felétlenül szükséges olyan módszerek kidolgozása, melyekkel a három feltétel módosító hatása kiküszöbölhető, vagy javítható.

A felszíni célpont, a Nap és a műhold műszere közötti geometriai kapcsolatot (ld. 6. ábra) megadó „kétirányú reflektancia eloszlás-függvény” (Bidirectional Reflectance Distribution Function, BRDF) segítségével a Nap és a műhold helyzetétől függetleníthetővé tehető a reflektancia-számítás. Ez a BRDF függvény nagymértékben függ a felszín borítottságától illetve a vegetáció tulajdonságaitól (például egy erdő a fák és a Nap magasságától függően vetít árnyékot a mellette levő alacsonyabb növényállományra, vagy akár a csupasz földre). Mivel a célterület környezete – a szomszédos pixelek – szintén meghatározó, ezért a függvény pontos meghatározása gyakorlatilag csak nagyobb homogén területekre lehetséges. Adott célterületre vonatkozó reflektancia-számításokat e BRDF függvény meghatározásával is végezhetünk (pl. Wu et al., 1995). Bizonyos származtatott mennyiségek sokkal kevésbé függnek a mérés geometriai tulajdonságaitól, mint a látható és a közeli infravörös csatorna reflektanciái. Ilyen például a normalizált vegetációs index, az NDVI (Normalized Difference Vegetation Index) abban az esetben, ha a képpont teljesen felhőmentes volt (Kimes et al., 1984; Holben et al., 1986; Cihlar et al., 1994).

A reflektanciából levezethető az a radiancia-érték, amely a Napból eredő rövidhullámú sugárzás felszínről visszaverődő része. Ennek kiszámításához egyrészt ismernünk kell a mérőműszer adott csatornájára vonatkozó hullámhossztartomány szélességét, másrészt azt a Napból eredő sugárzási áramsűrűséget (irradiancia), mely a felszínt eléri. A hullámhossztartomány szélességét az omega ekvivalens szélességgel adhatjuk meg, melyet a következő képlettel definiálunk:

(3)

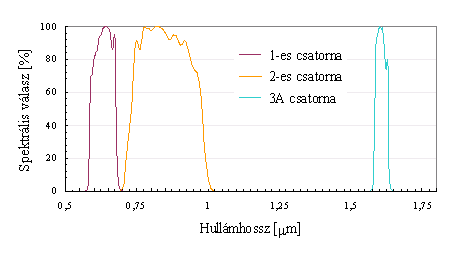
ahol Tau-lambda a relatív válaszfüggvény lambda hullámhosszhoz tartozó értéke (%-ban), lambda1 és lambda2 pedig rendre az alsó és a felső levágási hullámhosszak (mikrométer), melyek megadják a teljes hullámhossztartományt. A spektrális relatív válaszfüggvény fejezi ki, hogy a sugárzásmérő műszer az érzékelőjébe érkező sugárzást adott hullámhosszon hány százalékban képes felfogni (15. ábra).

Az F irradianciát (Wm-2), vagyis a felszínt elérő, Napból eredő sugárzási áramsűrűséget, az Flambda monokromatikus irradiancia (W m-2 mikrométer-1) teljes tartományra történő kiintegrálásával állíthatjuk elő, ahol a súlyozás a relatív válaszfüggvény (Tau-lambda) felhasználásával történik:

(4)

Ekkor a R-lambda-e (W m-2 sr-1 mikrométer-1) radiancia – vagyis az egységnyi idő alatt, egységnyi felületet elhagyó sugárzási energia a műszer által egységnyi térszögből érzékelve – a következő képlet segítségével számolható ki:

(5)

ahol ro jelöli a (2) alapján kiszámolt reflektanciát (%) egy adott pixelre, F a (4) szerint kiintegrált, és a spektrális válaszfüggvénnyel súlyozott irradianciát (W m-2), omega a spektrális válaszfüggvény ekvivalens szélességét (mikrométer). Az így kapott radiancia monokromatikus tulajdonságú, vagyis úgy tekinthető, mintha a sugárzást visszaverő felszín egy adott hullámhosszához tartozna ez az érték, nevezetesen az effektív hullámhosszhoz (lambdae). Ez az effektív hullámhossz a műszer mérési csatornájára jellemző érték, mely a hullámhossz tartomány közepén található. Pontos helyzetét az újonnan bevezetett mennyiségek segítségével a következő képlet adja meg:

(6)

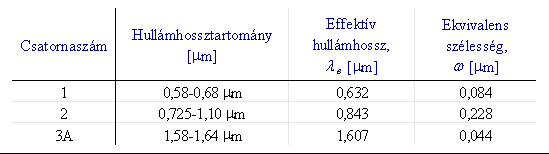
Példaként a 10. táblázatban a NOAA-15 műhold AVHRR/3 műszerére vonatkozó lambda és omega értékeket mutatjuk be.

10. táblázat
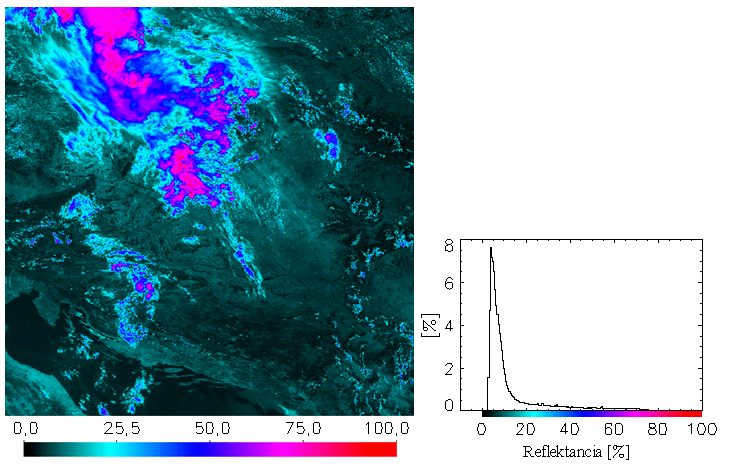
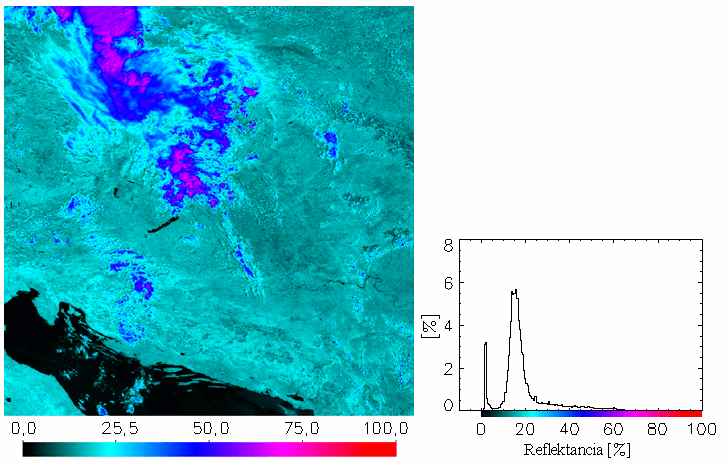
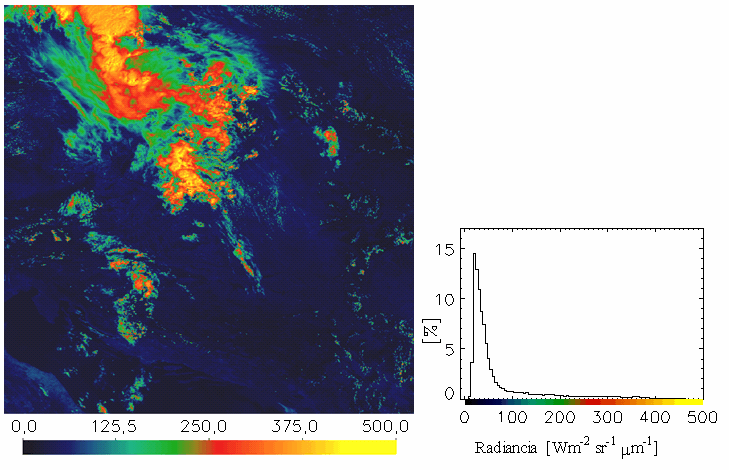
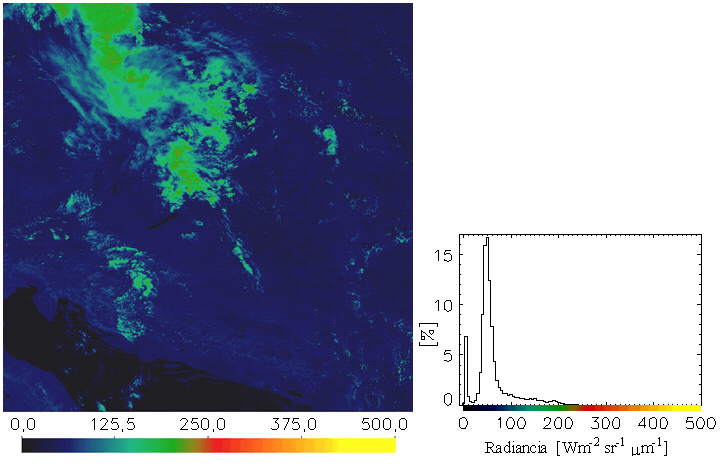
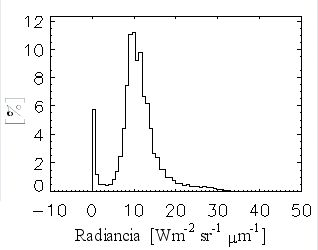
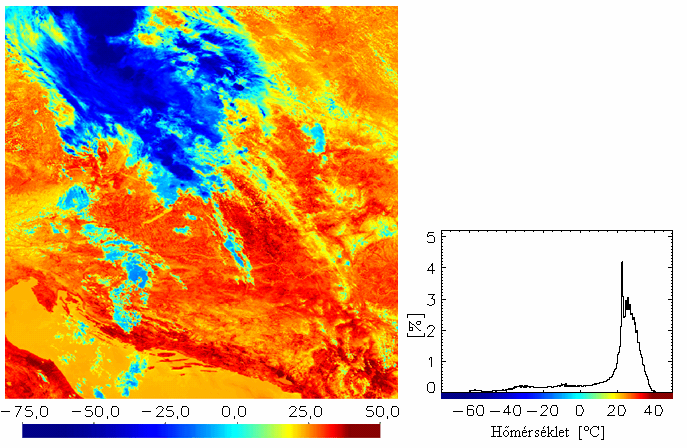
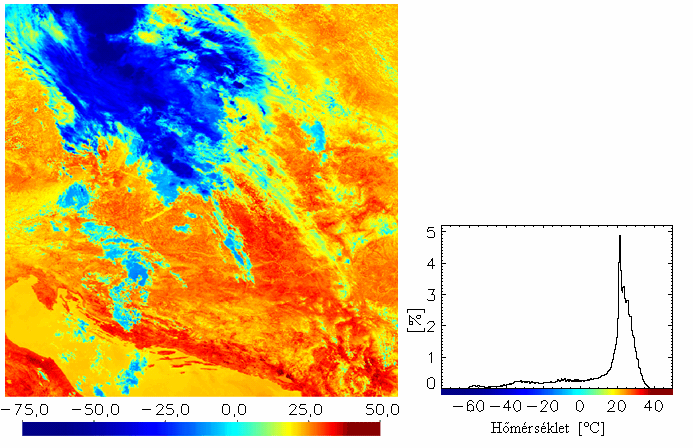
A NOAA-15 műhold első három csatornájára vonatkozó spektrális értékek

A fenti radianciaszámítás eredményeként előálló képeket és hisztogramokat az 19.-21. ábrákon mutatjuk be a NOAA-17-es műhold 2003. július 22-ei áthaladására. A hisztogramokon az adott képi pixelek 5 Wm-2 sr-1 mikrométer-1-ként lettek csoportosítva, az előfordulásuk gyakoriságát pedig %-ban adtuk meg. A képek egymással való összehasonlíthatóságát szem előtt tartva a skálabeosztáson nem változtattunk, melynek következtében azonban a 2-es és a 3-as csatorna képei túlságosan sötétek lettek. A hisztogram tanulmányozásakor figyelembe kell venni az alábbiakat is: Tekintve, hogy ezek a Kárpát-medencét tartalmazó kivágatok 1024×1024 pixelesek, az egész kép 1024**2, azaz 1 048 576 képi adatból áll. Így ahhoz, hogy a hisztogramon egy csoport már láthatóvá váljon, el kell, hogy érje a kb. 0,1 %-t, vagyis abban az adott tartományban legalább 1048 értéknek kell esnie. A képeken látható, hogy leginkább a kis reflektanciájú területek vannak túlsúlyban, melyek csak kevés sugárzást vernek vissza.

19. ábra
Kalibrációval kapott radianciakép [Wm-2 sr-1 mikrométer-1] az AVHRR 1-es, látható csatornájából
(0,58-0,68 mikrométer) és a hozzátartozó hisztogram / NOAA-17, 2003.07.22 09:31, 1-es csatorna /

20. ábra
Kalibrációval kapott radianciakép [Wm-2 sr-1 mikrométer-1] az AVHRR 2-es, látható csatornájából
(0,725-1,00 mikrométer) és a hozzátartozó hisztogram / NOAA-17, 2003.07.22 09:31, 2-es csatorna /

A 3A közeli infravörös csatorna szűk érzékenységi spektruma miatt (22. és 15. ábra) csak nagyon keskeny tartományban ad radiancia-értékeket (21. ábra). Ezért ez a kép az előző színezési skálával gyakorlatilag teljesen sötét és értelmezhetetlen lenne (a kalibrációval kapott képet így nem mutatjuk be).

21. ábra
A 3A közeli infravörös csatorna kalibrációjából nyert, radianciára vonatkozó hisztogram
/ NOAA-17, 2003.07.22 09:31, 3A csatorna /

A műholdas mérések kutatási célú felhasználásához még további, ún. légköri korrekciós eljárásokra van szükség, melyek a légköri hatásokat, valamint a felszín, a Nap és a műszer egymáshoz viszonyítottelhelyezkedését veszik figyelembe.

22. ábra
A NOAA-15 műhold AVHRR/3 sugárzásmérő berendezés két látható és egy az egyik
infravörös csatornájának spektrális relatív válaszfüggvényei

Kalibráció a műhold fellövése után

Eredetileg az AVHRR sugárzásmérők rövidhullámú (1-es és 2-es) csatornáit kizárólag a felhőzet detektálásához tervezték azzal a céllal, hogy az aktuális időjárási helyzet kiértékelését és előrejelzését megkönnyítsék. Ennek következében a műszert nem szerelték fel olyan eszközökkel, melyekkel működése közben rutinszerűen elvégezhető lenne ezeknek a csatornáknak a kalibrációja. Csak később alakult ki az igény arra, hogy ezekből a mérésekből következtetni lehessen a felszín albedójára és vegetációjára is. A mérésekből származtatható értékek pontossága több tényezőn múlik, melyek együttesen az AVHRR által mért jel gyengülését okozzák. Ez az ún. effektív jelgyengülés három hatás eredőjeként áll elő (Koslowsky, 1997a):
(1) Az első a műszer fokozatos elöregedéséből ered, mely műholdanként és csatornánként változik, és általában évi 1-8 %-os jelgyengülést jelent évente (Rao et al., 1996, Koslowsky et al., 2001). Közvetlenül a műholdak fellövése után a műszerek érzékenységében egy kisebb mértékű csökkenés következik be, mely a műszer optikájára kicsapódó vízpárának és a rakéta üzemanyagából hátramaradó szennyezőanyag lerakódásának a következménye.
(2) A második tényező alatt értjük a légkör sugárzásgyengítő hatását, melyet a különböző vastagságú légköri metszetek jelentenek a Nap látszólagos elhelyezkedését jellemző zenitszögétől függően. Még ha a felszíni célponthoz képest azonos zenitszögű áthaladásokat is tekintünk, az idő múlásával akkor is felfedezhető egy trendszerű viselkedés, mely az AVHRR által felfogott sugárzás változását idézi elő. Bár a kvázipoláris műholdak pályája napszinkron, vagyis a Naphoz viszonyított helyzetük állandó, mégis egy év alatt kb. fél óra késés jelentkezik pályájukon. Ez különösen az ún. délutáni műholdak esetében mutatkozik meg (melyek áthaladásai helyi idő szerint mindenhol délutánra esik), s nem csak az AVHRR-t érő sugárzás csökkenését jelenti, hanem hatással van a kétirányú reflektancia eloszlás-függvényre is. Egyéb légköri hatások is befolyásolhatják a sugárzásmérést (pl. vulkánkitörés okozta légköri aeroszol-többlet, Pinatubo, 1991). E pontatlanságokat légköri korrekciós eljárásokkal kell kiküszöbölni.
(3) A harmadik hatás a felszín anizotropitásából ered, s az évszakosan bekövetkező periodikusan változó megvilágítottság hatására áll elő. Az említett hatások miatt a fellövés előtt megállapított kalibrációs együtthatók már nem alkalmazhatók az operatívan működő műszerre.

A látható és közeli infravörös csatornák műholdon zajló kalibrációjához szükséges eszközök hiánya olyan helyettesítő eljárások fejlesztését eredményezte, melyek a műhold fellövését követően is elvégezhetők. A kidolgozott helyettesítő eljárásokkal (Mitchell et al., 1996; Rao és Chen, 1995) a TIROS-N műholddal (1978) kezdődő NOAA műholdsorozat AVHRR műszereinek két látható csatornájának működése jellemezhető és az így kapott eredmény kivetíthető a KLM sorozat AVHRR/3 műszereire is. A helyettesítő eljárások általában valamilyen külső referenciaméréseken alapulnak, melyekhez felhasználhatnak sugárzásméréstanilag viszonylag stabil földfelszíni célokat, csillagászati célokat, kalibrált sugárzásmérőket vagy modellezett radianciákat. Stabil földi célként a módszerekben sivatagokat alkalmaznak. Ennek legfontosabb oka, hogy a nagy kiterjedésű és hosszú ideje létező sivatagok albedója több tízéves időskálán állandónak tekinthető, továbbá a sivatagos területek felett általában kisebb a földfelszínt takaró felhőzet mennyisége, mely meggátolná a felszínre vonatkozó reflektancia-számításokat (Rao et al., 1999). Csillagászati célként egyes csillagok látható tartományba eső sugárzását vagy a Hold által visszavert napsugárzást lehet alkalmazni a kalibrációhoz. Ezt a módszert az AVHRR esetén még nem alkalmazzák, tesztelése a jövőbeli kutatási tervek közé tartozik. Kalibrált sugárzásmérőként a Terra műhold MODIS (Moderate Resolution Imaging Spectrometer) sugárzásmérő műszere által mért sugárzási adatok használhatóak fel (Heidinger et al., 2002). Az elsődlegesen alkalmazott utókalibrációs eljárásokban sivatagi célterületeken mért sugárzási értékek segítségével végzik el a kalibrációt azonos helyzetű áthaladások segítségével, hogy így kövessék a műszer állapotának változását az idő előrehaladtával. A NOAA laboratóriumaiban Rao és Chen (1995), illetve Rao et al. (1999) által kidolgozott módszerekkel végzik el a NOAA meteorológiai műholdak AVHRR műszereinek utólagos kalibrációját. Az általuk kidolgozott eljárás a Líbiai-sivatag dél-keleti részének egy kicsiny területét (Északi szélesség: 21-23°, Keleti hosszúság: 28-29°) veszi alapul. Számításaik során annak a spektrális válaszfüggvénynek az időbeli változását követik nyomon, mely a műszer reakcióját fejezi ki az adott területről érkező sugárzásra. Az ausztrál CSIRO intézetben Mitchell et al. (1997) a dél-ausztrál Strzelecki-sivatagot használják fel ugyanerre a célra.

Elsőnként a NOAA-15 műholdat szerelték fel az újabb fejlesztésű AVHRR/3 műszerrel, melynek válaszfüggvényének tanulmányozásához fontosak voltak a korábbi AVHRR berendezések segítségével szerzett tapasztalatok. Ellentétben az AVHRR/2 sugárzásmérővel, az AVHRR/3 reflektancia számítása két lineáris részből tevődik össze a beütésszám nagyságától függően ezért a két tartományra külön-külön kell megállapítani a (2) egyenlethez szükséges együtthatókat. Továbbá ezekkel az utókalibrációs technikákkal az érzékenységhez szükséges beütésszám-határok pontos értékei is megfelelően módosíthatóak. A reflektancia-számításra vonatkozó együtthatók havonkénti frissített értékei 1996 óta folyamatosan megtalálhatóak az Interneten (NOAASIS, 2004).

A NOAA-16 műhold esetében az utólagos kalibrációt a Líbiai- és a Takla Makán-sivatag (mely az ázsiai Tien-San-hegységtől délre fekszik) segítségével végzik el (NOAASIS, 2004). A műszerek törvényszerű elöregedése ellenére a NOAA-16 1-es és 2-es csatornájára még a fellövés előtt megállapított együtthatókat ajánlják, melyekkel a számított reflektancia közelítőleg megegyezik a valóssal. Mivel a 3A csatorna új a KLM-sorozat műholdjain, s így nincsenek erre vonatkozó korábbi mérésekből származó empirikus együtthatók, ezért ennél a csatornánál inkább a MODIS mérésekből számolt konstansokat ajánlják a reflektancia kiszámításához. Becslések szerint a MODIS mérésekből számolt reflektancia-értékek a ténylegesnél magasabbak. 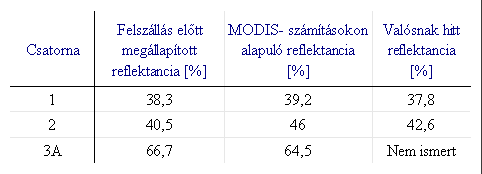A különböző módon megállapított reflektancia-értékeket a 11. táblázatban hasonlítjuk össze.

11. táblázat
A Líbiai-sivatagra vonatkozó reflektancia-értékek összehasonlítása NOAA-16 látható és közeli infravörös csatornáinak illetve MODIS mérések segítségével

A NOAA-17 műhold utókalibrációi még nem teljesek, s így nem is publikáltak, hiszen fellövése óta szűk két év telt csak el.

A termális infravörös csatornák kalibrálása

A termális infravörös csatornák kalibrációja az AVHRR/3 műszerek esetében a 3B, a 4-es és az 5-ös csatornák kalibrációját jelenti (8. táblázat). Az AVHRR/3 3B csatornája megegyezik a korábbi AVHRR változatok (AVHRR/1, AVHRR/2) 3-as csatornájával, hisz azokon a sugárzásmérőkön ez a csatorna állandóan üzemel, az AVHRR/3 esetében azonban csak éjszaka. A termális csatornákkal az infravörös sugárzási tartományban mérnek, azaz nem a visszavert napsugárzást érzékelik, hanem azt a hosszúhullámú sugárzást, melyet a vizsgált felszíni célpont és a felette elhelyezkedő légréteg bocsát ki hőmérsékletüktől függően. Így a kalibráció után a 3B csatornán mért adatokból éjszakai felhőészlelésre, a 4-es és 5-ös csatorna adataiból pedig a felhőzet azonosítására és a felszínhőmérséklet számítására nyílik többek között lehetőség.

A termális csatornák beütési száma és a kalibrált fekete test sugárzása közötti kapcsolatot megadó átviteli függvény, mint látni fogjuk, csak a 3B csatornára lineáris, így a 4-es és az 5-ös csatorna esetén nem-lineáris korrekciók alkalmazása is szükséges.
A kalibráció elméleti hátterét a Planck-függvény képezi:

(7)

melynek invertálásával az adott v hullámszámhoz (m-1) tartozó monokromatikus radianciából (Rv(T)) (W m-2 sr-1 m1) a vele ekvivalens hőmérséklet (T) kiszámítható. Az egyenletben szereplő univerzális állandók:
h = 6,62606876·10-34 J s, Planck-állandó
c = 2,99792458·108 m s-1, Vákuumbeli fénysebesség
k = 1,38065030·10-23 J K-1, Boltzmann-állandó
c1 = 1,1910427·10-5 mW m-2 sr-1 cm4
c2 = 1,4387752 cm K,
ahol c1 és c2 a (8) és a (9) egyenletekkel áll elő:

	(8)
	(9)

Kalibráció a műhold fellövése előtt

Az előkalibrációt az űrbeli sugárzási körülményeket szimuláló vákuumkamrában végzik. A sugárzásmérőt egymás után három abszolút fekete testre irányítják: (1) egy hideg célra, mely 95 K hőmérsékletével a világűrt képviseli, (2) egy laboratóriumi fekete testre, mely a Föld sugárzását utánozza, s (3) egy meleg fekete testre, mely a belső kalibrációs célt képviseli (12. táblázat). Mind a belső, mind a külső hőmérsékleteket platina ellenállás-hőmérőkkel (Platinum Resistance Thermometers, PRT) mérik. A mért hőmérsékletekből kiszámolják a sugárzási értéket minden termális csatornára vonatkozóan úgy, hogy az AVHRR kimenő jelei (a beütésszámok) 10 bites formátumúak legyenek, 0-tól 1023-ig terjedő tízes számrendszerbeli értékekkel. A skála fordított irányú, vagyis kisebb beérkező sugárzás (alacsonyabb hőmérséklet) esetén kapunk nagyobb kimenő jelet.
Az egész előkalibrációs ciklust többször (3-5 alkalommal) megismétlik. Mindegyik alkalommal a műszert egy másik hőmérsékletre állítják be a PRT-k segítségével 10 és 30 °C között. Ez a hőmérsékleti tartomány megegyezik azzal a tartománnyal, amit a pályáján haladó műszerben a belső kalibrációs cél felvehet. Ez utóbbit elektromos fűtőszálakkal 15 és 20 °C közötti hőmérsékleten próbálják tartani, melyet a PRT-kel pontosan megmérnek. A hőmérsékleti tesztsorozatok során a laboratóriumi fekete test hőmérsékletét – mely a Földi célt képviseli – 15-17 különböző szintre állítják be 180 K és 335 K között, mely így lefedi azt a hőmérsékleti skálát, melyet a műszer a Földre tekintve valaha mérhet. Ezen kalibrációs fekete testeknek az összefoglalása látható a 12. táblázatban.

12. táblázat
A laboratóriumi kalibrációhoz felhasznált fekete testek
megfeleltetése a tényleges céloknak

Kalibráció a világűrben

Az eltérő körülmények miatt a laboratóriumi mérések alapján meghatározott kalibrációs függvények és együtthatók csak részben alkalmazhatók a sugárzásmérő űrbeli működése során. A felbocsátás után folyamatos referencia-mérésekkel kontrolálják a kalibrációt. Ehhez a világűrt (mint abszolút fekete testet) és egy belső kalibrációs fekete testet használnak fel úgy, hogy állandóan mérik a sugárzásukat és az utóbbi hőmérsékletét. Ezen referencia-mérésekkel mindegyik termális csatornára meghatároznak egy kalibrációs görbét, melyből utána bármelyik beütésszámhoz megállapítható a hozzá tartozó sugárzásérték. Ezt a kalibrációs folyamatot mutatjuk be a következőkben.

Az AVHRR szenzora minden egyes földfelszíni sáv letapogatásakor elsőnként a világűrbe tekint ki (ennek sugárzásából előállít csatornánként tíz darab 10 bites beütésszámot), majd a 2048 pixeles (vagyis 2048 beütésszámból álló) földfelszíni letapogatott sáv után a belső kalibrációs test sugárzására vonatkozó értékek következnek (újabb tíz darab 10 bites beütésszám csatornánként). Az AVHRR műszer tükrének folyamatos forgásának következtében a következő földfelszíni sor letapogatása előtt újból a világűrre vonatkozó méréssel kezdődik a ciklus. A letapogatás során mért értékek kalibrációjához azért használatos ez a két kalibrációs fekete test, mert sugárzási értékeik közé egyértelműen kifeszíthető a Föld felszínéről 2048 pixelen érzékelt teljes sugárzási spektrum.

A világűr hőmérséklete ismertnek és állandónak tekinthető (12. táblázat), a belső fűtött kalibrációs fekete test hőmérsékletét (TBB) négy ellenállás hőmérővel (PRT) mérik, melyek az AVHRR műszerbe vannak beágyazva. A felszíni vevőkhöz továbbított információk fejlécében minden sor (mely egy adott letapogatott sávra vonatkozik) 18., 19. és 20. eleme a négy beépített PRT közül az egyikhez tartozó három különböző mérés eredménye. Négy soron keresztül mindig másik PRT méréseit adják meg, majd az ötödik sorban nullával jelzik a ciklus végét. Jelöljük CPRTi-vel az egy sorban található i. PRT-re vonatkozó három leolvasás átlagát. Ekkor egy negyedfokú képlet segítségével kiszámolható az adott platina ellenállás-hőmérő TPRTi hőmérséklete:

(10)

A d0, d1, d2, d3 és a d4 együtthatók értékei hőmérőnként és műholdanként csak nagyon kismértékben térnek el egymástól. A NOAA-15 és -17 műhold esetén a d3 és d4 értékei nullával egyenlők. A négy hőmérő méréseiből előálló TPRT1, TPRT2, TPRT3, TPRT4 hőmérsékletek számtani közepével adható meg a belső kalibrációs fekete test TBB hőmérséklete, melynek mértékegysége Kelvin:

(11)

A belső kalibrációs fekete test így kapott TBB hőmérsékletéből meghatározható a rá vonatkozó NBB radiancia, mely az adott csatornához tartozó spektrális válaszfüggvénnyel súlyozott Planck-függvény átlagos értéke. Ezt a számítást azonban jelentősen le lehet egyszerűsíteni a következő módon. A spektrális válaszfüggvényt minden egyes csatornára előre megállapítják kb. 200 darab hullámhossztartomány segítségével, mely alapján minden csatornára külön-külön táblázatban (energia-táblázat) megadják a 180 K és 340 K közötti 0,1 K-fokonkénti hőmérsékletekhez tartozó radiancia-értékeket. A (12) és (13) egyenletek kielégítő pontossággal visszaadják az energia-táblázatokban szereplő hőmérsékleteket a 180-340 K tartományban:

(12)

ahol TBB* az effektív fekete test hőmérséklete, A és B pedig csatornától és műholdtól függő együtthatók,

(13)

ahol a c1 illetve c2 pedig az úgynevezett első és második univerzális sugárzási állandó, melyek a (8) és a (9) egyenlet alapján számolhatóak, vc pedig az adott csatornához tartozó súlyozott hullámszám. Ennek (vc) reciproka megközelítően az adott termális csatorna hullámhossz-tartományának középértéke.
A két kalibrációs céltest (a belső kalibrációs fekete test, és a világűr) szolgál arra, hogy sugárzási beütésszámuk és a hozzájuk tartozó mért hőmérsékletek ismeretében lineáris becsléssel pixelenként kiszámítsuk a Földi sugárzási beütésszámokhoz tartozó hőmérsékleteket. Minden leképezési sor végén az AVHRR szenzora a belső kalibrációs fekete testre néz, és ekkor mind a három termális csatornához tíz-tíz beütésszámot mér, melyek a HRPT fájl fejlécének 23. és 52. szava között kerülnek tárolásra. Amikor pedig a műszer a világűr felé néz, mind az öt AVHRR csatornával szintén tíz-tíz beütésszámot mér. Ezek foglalják el a fejléc 53. és 102. szavai közötti helyeket (13. táblázat).

13. táblázat
A HRPT leképezési soraihoz tartozó fejlécek kalibrációs része

A csatornánként mért tíz-tíz kalibrációs érték átlagával a váratlanul fellépő zajokat simíthatjuk ki. A látható és közeli infravörös csatornákra vonatkozó értékekre és átlagaikra a kalibrációs eljáráshoz nincs most szükség. A belső kalibrációs fekete test átlagos beütésszámát (CBB), radianciáját (NBB), valamint a világűr átlagos beütésszámát (CS) és radianciáját (NS) felhasználva csatornánként előállítható a lineáris radiancia (NLIN):

(14)

ahol CE jelöli az AVHRR műszer által mért beütésszámot a 2048 földi pixel valamelyikére vonatkozóan. Mivel minden egyes sorban a négy platina ellenállás-hőmérő közül csak az egyik hőmérő által megmért hőmérsékletek találhatók meg, s így a belső kalibrációs fekete test hőmérsékletének meghatározásához (mely átlagolással történik) négy sorra van szükség, továbbá mivel minden ötödik sorban 0 értékek állnak a platina-ellenállás hőmérők számára fenntartott helyeken, így erre az öt sorra kell kiterjeszteni a korábbiakban megállapított NBB radiancia-értéket.

Az adatsorokban időnként előforduló hibák miatt a HRPT-fájl felépítése nem mindig ilyen szabályszerű. Vételi vagy egyéb hiba miatt kimaradhat egy vagy akár több teljes sor is, mely az AVHRR mérési eredményeken túl a fejléceket, s bennük a kalibrációhoz szükséges értékeket, így a platina-ellenállás hőmérők adatait is tartalmazná. Ezen PRT-vel mért hőmérsékletek hiányában nem lehet a megszokott pontossággal megadni a belső kalibrációs fekete test hőmérsékletét az adott pár sorra vonatkozóan. Ilyenkor az előtte és mögötte lévő átlagolt hőmérsékletek alapján interpolációval pótoljuk hozzá a csonkított tömbhöz a szükséges hőmérséklet-értékeket. Ez a probléma legtöbbször a teljes műholdkép elején és végén jelentkezik, de tapasztalataink alapján előfordulhat a kép közepén is, vagyis akár abban a kivágatban, melyet az eredeti képből archiválás és feldolgozás céljából rutinszerűen kivágunk. Így ennek a hibaforrásnak a folyamatos ellenőrzése is indokolt.

Az AVHRR 3B csatornájának indium-antimon érzékelője (Labrot et al., 2003) lineárisan reagál a bejövő sugárzásra, így nincs szükség nem-lineáris korrekciókra, s az NS radiancia értéke erre a csatornára nullával egyenlő. Ezzel ellentétben a 4-es és az 5-ös csatorna higany-kadmium-tellurid érzékelői a bejövő sugárzásra nem-lineáris választ adnak, s így az NS radianciák értékei nullától eltérőek lesznek. A fellövés előtti laboratóriumi mérések alapján állíthatjuk, hogy a mérni kívánt földfelszíni cél radianciája az AVHRR beütésszámait leírónégyzetes függvény a lineáristól csak kis mértékben tér el. E függvénynél a nem-linearitás mértéke az AVHRR működési hőmérsékletétől függ. Feltételezték, hogy ez a nem-lineáris viselkedés a pályáján haladó műhold esetében is megmarad, ezért a következő korrekciós módszert alkalmazhatjuk. Először az NLIN lineáris becslést kell kiszámolni a (14) egyenlet alapján az adott csatornához tartozó a világűrre vonatkozó NS radianciával. Majd pedig eme nem-lineáris radiancia segítségével a következő négyzetes korrekciót alkalmazva előállítható az NCOR nem-lineáris korrekciós érték:

(15)

ahol a b0, b1 és b2 négyzetes együtthatóinak értékei csatornától és műholdtól függő konstansok. A Földi pixelről az érzékelőbe jutó NE sugárzás értékét a fenti két érték (NLIN és NCOR) összegeként állíthatjuk elő:

(16)

Így a nem-nulla űrsugárzás bevezetése (NS) egy elméleti eszköz, melyet két dolog indokol. Egyrészt alkalmazásával csatornánként csak egyetlen egy négyzetes korrekciós egyenletre van szükség, hiszen a négyzetes együtthatók függetlenek az AVHRR működési hőmérsékletétől. Másrészt pedig ezzel a módszerrel nagyon jól rekonstruálhatjuk a fellövés előtti méréseket, a négyzetes középérték különbségek a mért és az illesztett adatok között kb. 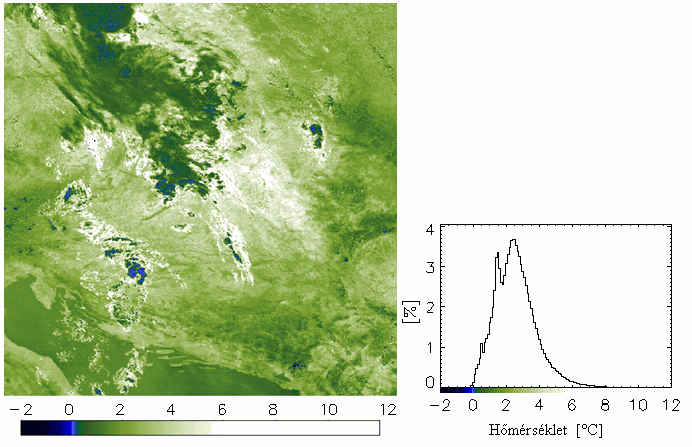0,1 K mind a 4-es és az 5-ös csatornára.

Végül a fentiek alapján kapott NE pixelenkénti sugárzási értékeket átalakítjuk a velük egyenértékű TE fekete test hőmérsékletekké, melyeket a Planck-függvény invertálásával kapott TE* effektív hőmérsékletekből számolhatunk minden termális csatornára (17) és (18) alapján:

	(17)
	(18)

ahol a c1, c2 univerzális állandók, vc, A és B együtthatók pedig a korábbiakban szerepelt műholdtól illetve csatornától függő állandók.

A (18) egyenlettel megkaptuk az adott csatorna képi pixeleihez tartozó hőmérsékleteket. A fentiekben ismertetett felszíni hőmérsékletet számító algoritmus eredményeit mutatjuk be a 23-25. ábrákon a NOAA-17-es műhold 4-es és 5-ös csatornájának mérései alapján a 2003. július 22-ei áthaladása esetére. A hisztogramokon az adott képi pixelek 0,5 °C-onként lettek csoportosítva, s az előfordulásuk gyakoriságát %-ban adtuk meg. Az összehasonlításra alkalmas megjelenítéshez a két csatornából számított hőmérsékleti értékeket egy azonos skálára kellett lenormálni. Ennél a műholdképnél, amint az a 25. ábrán is látszik, a pixelek nagy többségénél a 4-es csatornából származtatott felszíni hőmérséklet magasabb volt az 5-ös csatornához képest, átlagosan 2-2,5 °C-kal. A magasabb felhőtetők esetében kisebb eltérés adódott a két csatornából számolt hőmérsékleti értékek között, mint a talajfelszínek esetén, a legmagasabb felhőtetők egy részénél az is előfordult, hogy az 5-ös csatornából számolt érték volt a magasabb.

23. ábra
Az AVHRR 4-es, infravörös csatornájának méréseiből a kalibráció után kapott
hőmérsékleti mező és a hozzá tartozó relatív gyakorisági hisztogram
/ NOAA-17, 2003.07.22 09:31, 4-es csatorna/



24. ábra
Az AVHRR 5-ös, infravörös csatornájának méréseiből a kalibráció után kapott
hőmérsékleti mező és a hozzá tartozó relatív gyakorisági hisztogram
/ NOAA-17, 2003.07.22 09:31, 5-ös csatorna/

25. ábra
Az AVHRR 4-es és 5-ös infravörös csatornájának méréseiből a kalibráció után kapott hőmérsékletek különbségi mezője illetve a hőmérséklet eltérésnek relatív gyakorisága
/ NOAA-17, 2003.07.22 09:31/

A termális csatornák sugárzási értékeiből előállított hőmérsékleti értékeket erősen befolyásolják a felszín és a légkör állapotán túl a mérés hullámhossz-tartománya és a műszer egyedi tulajdonságai. Ennek következtében a kiszámított földfelszíni hőmérsékletek nem egyeznek meg sem a különböző csatornákra, sem a tényleges földfelszíni hőmérsékletekkel. Általában a kalibrációval nyert hőmérséklet-értékek alábecslik a tényleges földfelszíni hőmérsékleteket, melynek az az oka, hogy a légkör tetején mért sugárzásnál a tényleges felszíni értékekhez a légkör hatása is hozzáadódik (elnyelésként vagy a felszín felé történő visszaverődésként). A légköri abszorpció (sugárzáselnyelés) és emisszió (kisugárzás) illetve a talaj emisszivitása (sugárzóképessége) csökkenti a korrelációt a felszín által kibocsátott sugárzás és a műholdon levő sugárzásmérőt ténylegesen elérő radiancia között, megnehezítve a felszínre vonatkozó hőmérsékletek kiszámolását. A levegőben történő sugárzás-elnyelésért és újra kibocsátásért a vízgőz és a légköri gázok közül elsősorban a CO2 felelős azokban a légköri ablakokban is, melyet az AVHRR/3 infravörös csatornái méréseikhez használnak. A felszín hatása pedig az, hogy az egyáltalán nem tökéletes hősugárzás-kibocsátó (azaz nem tökéletes fekete test) és ez a tökéletlenség is erős változékonysággal bír.

Ennek a problémának a megoldására az AVHRR sugárzásmérő berendezés adataiból a Föld felszíni hőmérsékletének minél pontosabb becslésére már számos módszer született (Becker és Li, 1990; Kerényi és Putsay, 2000; Sobrino et al., 1993; Ulivieri et al., 1992), de egyik eljárás sem használható univerzálisan. Ezen algoritmusok alapja az ún. split window módszer: a két egymáshoz közeli infravörös csatorna a légköri gázok különböző sugárzáselnyelését érzékeli, így a felszín hőmérséklete a két csatorna valamilyen lineáris kombinációjaként becsülhető meg:

(19)

Ebben az egyenletben egy adott pixelre TS jelöli a felszíni hőmérsékletet, Ti a kalibrációval meghatározható fényességi hőmérsékletet. Az a0 és ai együtthatók a légkör állapotától és a felszín emisszivitásától függnek. Időnként ezekre az együtthatókra bizonyos konkrét értékeket javasolnak, de ezek jelentős hibákat vonhatnak maguk után. A felszíni hőmérséklet előállításához tehát mindenképpen szükség van az infravörös csatornákra vonatkozó, a felszín emisszivitását valamilyen módon kifejező együtthatókra.