Fluxes calculated by means of the similarity theory

The system was designed to enable us to calculate vertical flux of carbon dioxide from the long term profile measurements. The critical evaluation of the accuracy with which the fluxes can be determined will be given later.

Estimates of the vertical mass transport of CO and other scalars at the surface can be obtained by using surface layer (the lowest 10% of the planetary boundary layer) similarity theory (e.g., see Dyer and Hicks, 1970; Businger et al., 1971; Foken and Skeib, 1983; Businger, 1986; Stull, 1988; Yagüe and Cano, 1994; Saigusa et al., 1998; Hensen et al., 1997; Weidinger et al., 2000), if the vertical profiles of wind speed and air temperature are also available. Applicability of the similarity theory has several preconditions (see Foken and Wichura, 1996 for detailed overview). Briefly, the turbulent field must be horizontally homogeneous and stationary with an appropriate homogeneous area up to a distance of approximately (where is the measuring height) around the measuring site.

In our case, the unusually large height differences between the measuring levels cause uncertainty in the estimate of the similarity profiles but also contributes to improved estimates of the (often small) mixing ratio and temperature gradients. Difficulty arises during nighttime stable conditions when we are restricted to use data measured by the two lowest levels (10 m and 48 m) for the estimate of fluxes to ensure that the utilized data reside in the surface layer (Stull, 1988; Yagüe and Cano, 1994). During unstable conditions we use data of the three lowest levels, up to 82 m height. At night, the 82 m level is often above the inversion layer, and so it is completely decoupled from the ground. Also, the precondition of homogeneous fetch is not fulfilled in our case. Consequently, the results acquired from the similarity theory are expexted to have errors.

As there are three measuring levels located inside the surface layer during unstable conditions, the surface layer fluxes can be inferred using profile fitting technique instead of the less precise flux-gradient relationships which utilize data from only two levels.

According to the Monin-Obukhov similarity theory, the non-dimensional wind, temperature, and scalar profiles can be expressed in the horizontally homogeneous and stationary surface layer as:

$$\phi _{m}(\frac{z}{L})=\frac{kz}{u_{*}}\frac{\partial u}{\partial z}\: ,$$ (2.5)

$$\phi _{h}(\frac{z}{L})=\frac{kz}{\theta _{*}}\frac{\partial \theta }{\partial z}\: ,$$ (2.6)

$$\phi _{s}(\frac{z}{L})=\frac{kz}{s_{*}}\frac{\partial s}{\partial z}\: ,$$ (2.7)

or with the integrated forms as :

$$u=\frac{u_{*}}{k}[\ln \frac{z}{z_{0}}-\psi _{m}(\frac{z}{L})]\: ,$$ (2.8)

$$\theta -\theta _{0}=\frac{\theta _{*}}{k}[\ln \frac{z}{z_{0}}-\psi _{h}(\frac{z}{L})]$$ (2.9)

$$s-s_{0}=\frac{s_{*}}{k}[\ln \frac{z}{z_{0}}-\psi _{s}(\frac{z}{L})]\: ,$$ (2.10)

with

$$\psi _{m}\left( \frac{z}{L}\right) =\int ^{z/L}_{z_{0}/L}\frac{\left( 1-\phi _{m}\right) }{\zeta }d\zeta \: ,$$ (2.11)

$$\psi _{h}\left( \frac{z}{L}\right) =\int ^{z/L}_{z_{0}/L}\frac{\left( 1-\phi _{h}\right) }{\zeta }d\zeta \: ,$$ (2.12)

$$\psi _{s}\left( \frac{z}{L}\right) =\int ^{z/L}_{z_{0}/L}\frac{\left( 1-\phi _{s}\right) }{\zeta }d\zeta \: ,$$ (2.13)

where , and are mean quantities of horizontal wind speed, potential temperature ( , where is the absolute temperature) and scalar mixing ratio (e.g. water vapor or any other trace gas) at height above the zero plane displacement, is the surface potential temperature, (Högström, 1996) is the von Kármán constant, z is the roughness length, , and are the dimensionless wind shear, temperature and scalar concentration gradients respectively, is the friction velocity (defined as with is the Reynolds' stress and is the air density), is the temperature scale ( ), is the scalar scale ( ), with is the Obukhov length:

$$L=\frac{u^{2}_{*}\overline{T}}{kg\theta _{*}}\: ,$$ (2.14)

where is the reference absolute temperature for the surface layer (calculated as the average temperature of the surface layer from the temperature profile measurements) and . Note that the water vapor buoyancy correction is neglected for the calculation of (Högström, 1988).

It is generally accepted that since for both potential temperature and other scalars the turbulent exchange is governed by the same turbulent field thus the physical process of the transport is similar.

The functional forms of and are determined by field measurements (Högström, 1988). Due to the large scatter of the experimental data many different functions can be found in the literature (e.g. Dyer, 1970; Businger et al., 1971; Foken and Skeib, 1983; Högström, 1988, 1996; Weidinger et al., 2000). For our purposes the revised similarity functions of Högström (1996) are used, which are best fits to large quantities of experimental data. For unstable situations these are as follows:

$$\phi _{m}=(1-19\frac{z}{L})^{-1/4}\: ,$$ (2.15)

$$\phi _{h}=0.95(1-11.6\frac{z}{L})^{-1/2}\: ,$$ (2.16)

and for stable situations:

$$\phi _{m}=1+5.3\frac{z}{L}\: ,$$ (2.17)

$$\phi _{h}=0.95+8\frac{z}{L}\: .$$ (2.18)

Functions and are as follows for unstable conditions () after Benoit (1977):

$$\psi _{m}=\ln \left[ \left( \frac{1+x}{2}\right) ^{2}\left( ... ...}\right) \right] -2\arctan \left( x\right) +\frac{\pi }{2}\: ,$$ (2.19)

$$\psi _{h}=2\ln \left[ \frac{1+y}{2}\right] \: ,$$ (2.20)

where and .

For stable conditions ():

$$\psi _{m}=-5.3\frac{z-z_{0}}{L}\: ,$$ (2.21)

$$\psi _{h}=0.05\ln \frac{z}{z_{0}}-8\frac{z-z_{0}}{L}\: .$$ (2.22)

Note that = since .

Before the application of the profile fitting technique, wind direction dependent roughness length () is determined dividing the wind directions into 120 sectors (analogous to the wind direction classification of the eddy covariance system, see chapter ). The idea behind the calculation method is that surface layer fluxes can also be inferred from measurements taken at only two levels using flux-gradient relationships instead of the more precise flux-profile method. Flux-gradient relationships do not utilize since during the iteration the values of and are determined from two level's data thus is rejected (e.g. considering eq. for two different levels and substracting them will lead to an equation which does not contain ). After and had been determined eq. can be used to determine for a specific height, wind direction and wind speed:

$$z_{0}=z\exp \left[ -\frac{uk}{u_{*}}-\psi _{m}\left( \frac{z}{L}\right) \right] \: .$$ (2.23)

Values of are determined from the long term profile measurements classified by wind direction. Data measured during unstable atmospheric conditions are used, utilizing wind speed data from 48 m and 10 m. The calculated values are averaged in 3 degree intervals of the wind direction. Because of the huge scatter of data, only one average is used in each sector through the years. The average roughness length is 0.15 m, the minimum value is 0.06 m, and the maximum is 0.24 m.

For zero plane displacement m is used considering that the measuring tower is surrounded by arable land presumably with low vegetation. It should be noted that the calculations are not sensitive to the choice of since the measuring levels are located relatively high above the vegetation (Weidinger et al., 2000).

The algorithm of calculation is as follows.

First the bulk Richardson number is determined based on data measured by the two lowest level (Yagüe and Cano, 1994; Stull, 1988):

$$Ri\cong \frac{g}{\theta _{0}}\frac{\left( \theta _{2}-\theta... ...left( z_{2}-z_{1}\right) }{\left( u_{2}-u_{1}\right) ^{2}}\: ,$$ (2.24)

where is the acceleration due to gravity, subscript 2 indicates level 2 (48 m), and subscript 1 indicates level 1 (10 m).

Then, it is determined whether the situation was stable or unstable based on the potential temperature profile. This could be decided based on the bulk Richardson number, but the temperature profile may differ from the theoretical, strictly monotonous change with height especially during the morning transition period from stable to unstable stratification, thus at higher altitudes (e.g. at 82 m) the temperature value may not fit the lapse rate determined by the two lowest level. Also, during daytime, well-mixed conditions, the temperature profile is close to the dry adiabatic lapse rate (0.0098 K m), which means that small fluctuations of the average temperature at one level can cause deviations from the strictly monotonous profiles.

Next, initial Obukhov length is estimated which is required to start the iteration.

If the conditions are unstable is calculated based on the definition of the Obukhov length (eq. ) fitting to pure logarithmic profiles for a neutral atmosphere:

$$u=\frac{u_{*}}{k}\ln \frac{z}{z_{0}}\: ,$$ (2.25)

$$\theta -\theta _{0}=\frac{\theta _{*}}{k}\ln \frac{z}{z_{0}}\: .$$ (2.26)

is determined in the following manner. The applied procedure, which is widely used during the entire procedure, fits the paired data to the linear model, , by minimizing the Chi-square error statistics which is computed as the sum of squared errors divided by the standard deviations. The intercept of the line is forced to be zero because at height the wind speed theoretically becomes zero. The slope of the fitted line () then gives . For the similar determination of the surface value is also neccessary. The latter is determined using interval bisector technique for fast convergence. The technique fits many lines during the iteration for many different using the method described above storing the Chi-square error statistics for each fit. Then the surface value will be the value with the smallest Chi-square error. is calculated in the same way as since the temperature difference profile ( ) is already known. is estimated substituting and into eq. .

During stable conditions, is estimated from the bulk Richardson number (Yagüe and Cano, 1993) using Businger's similarity function (Businger, 1971):

$$F(Ri)=\frac{9.4Ri-0.74+\sqrt{4.88Ri+0.5476}}{9.5-44.18Ri}$$ (2.27)

and

$$L_{initial}=\frac{z_{2}-z_{1}}{\ln \frac{z_{2}}{z_{1}}F(Ri)}\: .$$ (2.28)

Iteration is starting with the value, using the least squares fit technique described above to obtain , and using equations and to determine the and values for the line fitting (instead of eq. and ). Again, the intercepts of the fitted lines are forced to be zero, and the slopes of the lines determine and . A new is calculated in each step from the new and values. As it was mentioned in the beginning of this chapter, for unstable conditions data measured by the lowest 3 levels are utilized for the fitting (10 m, 48 m and 82 m), and for stable conditions data measured by the two lowest levels are used to ensure that only data measured inside the surface layer is used.

The iterative method consists of comparing the new with the previously calculated one. Iteration finishes when the difference between two consecutive values is less then 1% of the current Obukhov length, or after 30 iteration steps.

During stable conditions the iteration can fail, due the strong stability. If this is the case, the analytical solution of Lee (1997) is used if the bulk Richardson number is less than 0.2. In other cases turbulence is supressed or tends to be intermittent, so the similarity theory is no longer applicable. The formulae of Lee is the following:

$$\frac{z}{L}=\frac{\frac{z}{z-z_{0}}\ln \left( \frac{z}{z_{0}... ...{2}}}\right] }{2\frac{\beta }{R}\left( \beta Ri-1\right) }\: ,$$ (2.29)

where the constants and are determined according to the similarity functions of Högström (1996) used here. is the geometrical height between the two lowest measuring levels defined as .

In case of successful iteration or analytical solution, the water vapor dry air mixing ratio (, given in g/kg dry air) and carbon dioxide dry air mixing ratio (, given in ppm, which is equivalent with mol/mol dry air) profiles are used to estimate and with the line fitting method described above using eq. .

Finally, the scales are converted to usual physical fluxes:

$$\tau =\rho u^{2}_{*\: ,}$$ (2.30)

$$H=-\rho c_{pd}\theta _{*}u_{*\: ,}$$ (2.31)

$$LE=-\rho L_{v}\frac{1}{1000}q_{*}u_{*\: ,}$$ (2.32)

$$F_{cp}=-\rho \frac{M_{CO_{2}}}{M_{d}}c_{*}u_{*}\: ,$$ (2.33)

where is the momentum flux (or Reynolds' stress in kg m s), is the sensible heat flux (in W m), is the latent heat flux (the energy flux equivalent of the vertical mass transfer of water vapor in W m), is the CO flux (in mg m s), is the density of air, is the specific heat of dry air, is the latent heat of vaporization (in J kg), is the molar weight of carbon dioxide and is the molar weight of dry air (in kg mol).

Since profile measurements are performed in every 8 or 10 minutes (see section ), the fluxes calculated from each available individual measurement are averaged to 60 minutes.

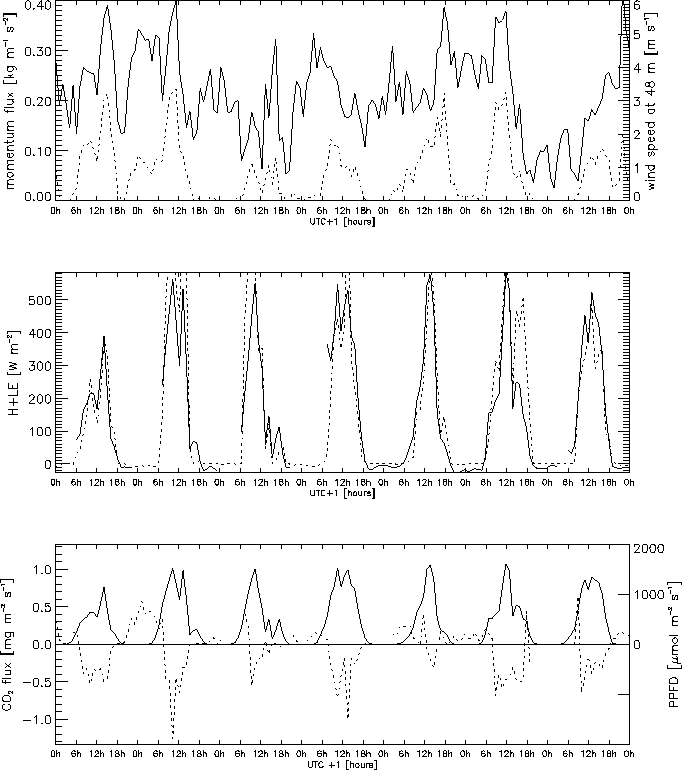
Figure shows one week of profile data together with some meteorological elements.

Figure: One week of profile flux data (11-17 July, 1997) together with some meteorological elements. Upper plot: average wind speed measured at 48 m (solid line) and the momentum flux (dashed line). Middle plot: The net radiation (solid line) and the sum of sensible and latent heat flux (dashed line). Lower plot: photosynthetically active photon flux density (PPFD, solid line), and the CO flux (dashed line).